Che cos'è "z" per un intervallo di confidenza dell'88%?

Se cerchiamo un intervallo di confidenza dell'88%, ciò significa che vogliamo solo una probabilità del 12% che il nostro intervallo non contenga il valore reale. Supponendo un test su due lati, ciò significa che vogliamo una probabilità del 6% attribuita a ciascuna coda del #Z#-distribuzione. Quindi, cerchiamo il #z_(alpha//2)# valore di #z_0.06#.

Questa #z# valore a #alpha//2 = 0.06# è la coordinata di #Z#-curve che ha il 6% dell'area di distribuzione alla sua destra, e quindi il 94% dell'area alla sua sinistra. Lo troviamo #z#-valore di ricerca inversa in a #z#-tavolo.

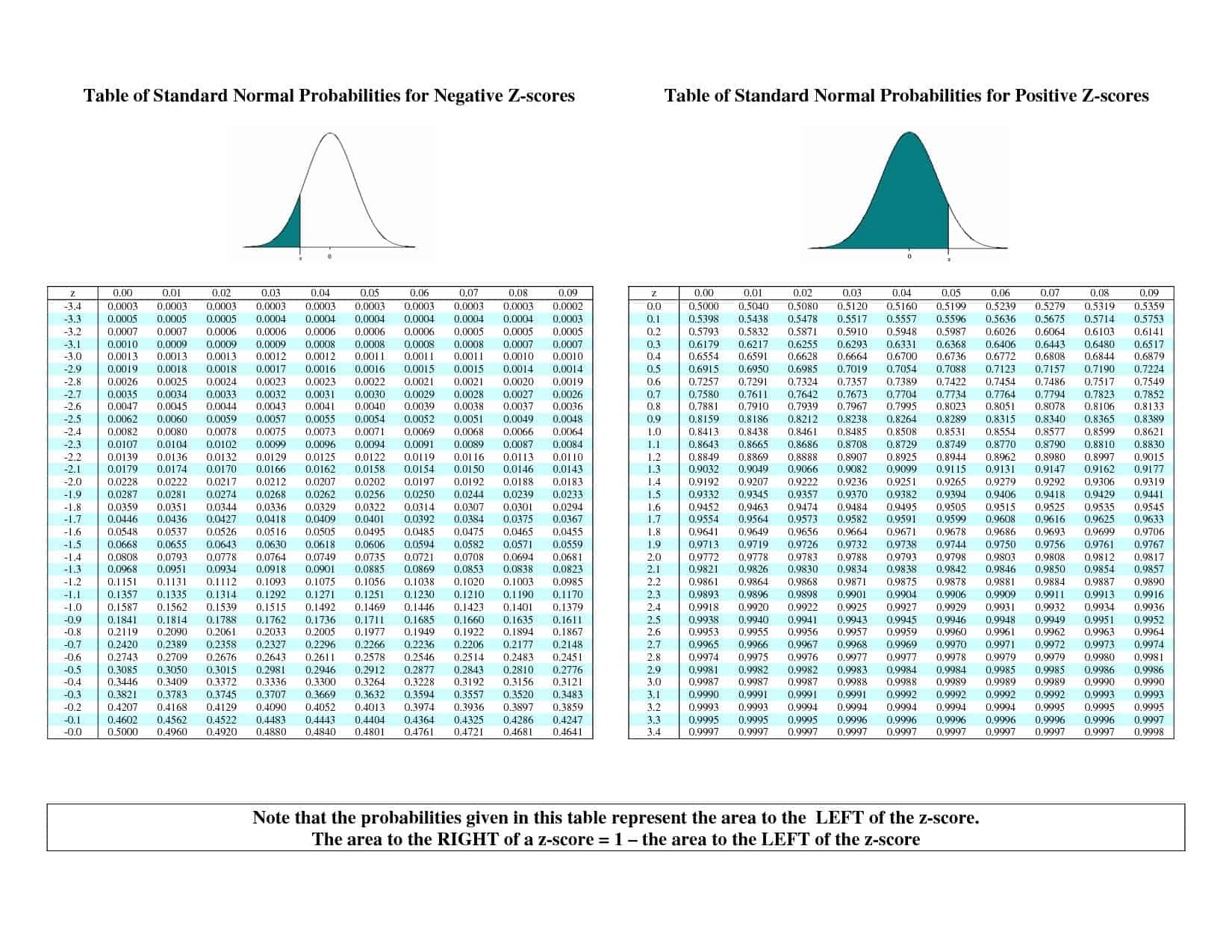
Trova il valore più vicino nella tabella a 0.9400 come puoi, quindi vedi qual è la sua riga e colonna. Dall'osservazione, vediamo che 0.9394 e 0.9406 sono nella tabella con #z#-valori rispettivamente di 1.55 e 1.56, e quindi per errare sul versante della prudenza, sceglieremo il valore che ci dà un intervallo più ampio, #z=1.56.#

Nota: Potremmo anche ottenere una risposta da software come R, digitando il comando #"qt(0.94, Inf)"#, che ci darebbe un valore più preciso di 1.554774.