Perché un trapezio è un quadrilatero, ma un quadrilatero non è sempre un trapezio?

Quando si considera la relazione tra due forme, è utile farlo da entrambi i punti di vista, ad es necessario vs sufficiente.

Necessario - #A# non può esistere senza le qualità di #B#.
Sufficiente - Le qualità di #B# descrivere sufficientemente #A#.

#A# = trapezio
#B# = quadrilatero

Domande che potresti voler porre:

1. Può esistere un trapezio senza possedere le qualità di un quadrilatero?
2. Le qualità di un quadrilatero sono sufficienti per descrivere un trapezio?

Bene, da queste domande abbiamo:

1. No. Un trapezio è definito come un quadrilatero con due lati paralleli. Pertanto, la qualità di "quadrilatero" è necessaria e questa condizione è soddisfatte.
2. No. Può avere qualsiasi altra forma quattro lati, ma se non ha (almeno) due lati paralleli, esso non può essere un trapezio. Un semplice controesempio è a boomerang, Che ha di preciso quattro lati, ma nessuno di loro è parallelo. Pertanto, le qualità di un quadrilatero non descrivono sufficientemente un trapezio e questa condizione è non soddisfatto.

Alcuni pazzi esempi di quadrilateri:

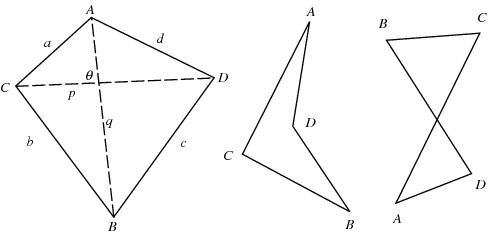
Ciò significa che un trapezio è troppo specifico di un quadrilatero che avere semplicemente la qualità di "quadrilatero" non garantisce la qualità di "trapezio".

Nel complesso, un trapezio is un quadrilatero, ma un quadrilatero non deve essere un trapezio.