Qual è la formula della superficie per una piramide rettangolare?

La superficie sarà la somma della base rettangolare e del #4# triangoli, in cui ci sono #2# coppie di triangoli congruenti.

Area della base rettangolare

La base ha semplicemente un'area di #lw#, poiché è un rettangolo.

#=>lw#

Area dei triangoli anteriore e posteriore

L'area di un triangolo si trova attraverso la formula #A=1/2("base")("height")#.

Qui, la base è #l#. Per trovare l'altezza del triangolo, dobbiamo trovare il altezza inclinata da quel lato del triangolo.

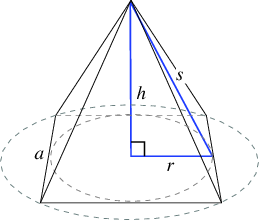
L'altezza inclinata può essere trovata risolvendo l'ipotenusa di un triangolo rettangolo all'interno della piramide.

Le due basi del triangolo saranno l'altezza della piramide, #h#e metà della larghezza, #w/2#. Tramite la teorema di Pitagora, possiamo vedere che l'altezza dell'inclinazione è uguale a #sqrt(h^2+(w/2)^2)#.

Questa è l'altezza della faccia triangolare. Pertanto, l'area del triangolo anteriore è #1/2lsqrt(h^2+(w/2)^2)#. Poiché il triangolo posteriore è congruente con quello anteriore, la loro area combinata è doppia rispetto all'espressione precedente, oppure

#=>lsqrt(h^2+(w/2)^2)#

Area dei triangoli laterali

L'area dei triangoli laterali può essere trovata in un modo molto simile a quello dei triangoli anteriore e posteriore, tranne per il fatto che la loro altezza inclinata è #sqrt(h^2+(l/2)^2)#. Pertanto, l'area di uno dei triangoli è #1/2wsqrt(h^2+(l/2)^2)# ed entrambi i triangoli combinati sono

#=>wsqrt(h^2+(l/2)^2)#

Superficie totale

Aggiungi semplicemente tutte le aree dei volti.

#"SA"=lw+lsqrt(h^2+(w/2)^2)+wsqrt(h^2+(l/2)^2)#

Questa non è una formula che dovresti mai tentare di memorizzare. Piuttosto, questo è un esercizio per comprendere veramente la geometria del prisma triangolare (oltre a un po 'di algebra).