Un blocco di 5 kg poggia su un'inclinazione di 30 °. Il coefficiente di attrito statico tra il blocco e l'inclinazione è 0.20. Quanto è grande una forza orizzontale che deve spingere sul blocco se il blocco deve essere sul punto di scivolare a) su per l'inclinazione, b) per l'inclinazione?

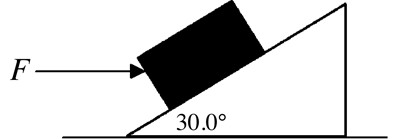
lasciare #F# applicare una forza orizzontale sul blocco come mostrato sopra. Questa forza avrà due componenti

(1) #Fcos30^@# che agirà verso l'alto parallelamente al piano inclinato.

(2) #Fsin30^@# che agirà perpendicolarmente sul piano inclinato. Quindi verrà aggiunto con il componente del peso del blocco #5gcos30^@# per aumentare l'entità della reazione normale #N#
Quindi la forza di attrito
#f_"fric"=muN=0.2(Fsin30^@+5gcos30^@)#, dove l'accelerazione dovuta alla gravità #(g) =9.8m"/"s^2#

Anche in questo caso il componente del peso del blocco di massa 5 kg che agisce verso il basso parallelamente al piano inclinato è #5gsin30^@#

(a) Considerando che l'equilibrio delle forze quando il corpo è sul punto di scivolare su per l'inclinazione possiamo scrivere

#Fcos30^@=5gsin30^@+0.2(Fsin30^@+5gcos30^@)#

#=>F=(5g(sin30^@+0.2cos30^@))/(cos30^@-0.2sin30^@)~~43N#

(b) Considerando che l'equilibrio delle forze quando il corpo è sul punto di scivolare giù per l'inclinazione, possiamo scrivere

#Fcos30^@=5gsin30^@-0.2(Fsin30^@+5gcos30^@)#

#=>F=(5g(sin30^@-0.2cos30^@))/(cos30^@+0.2sin30^@)~~16.6N#