Come si esprime cos (pi / 3) * cos ((pi) / 6) senza usare i prodotti delle funzioni trigonometriche?
Risposta:
La risposta finale è sqrt3/4
Spiegazione:
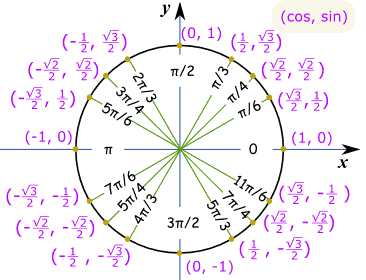
Per le funzioni Trig, ecco il tuo migliore amico, il cerchio trig.
Quello che vedi qui è per ogni sezione del cerchio che hai, c'è un valore per il coseno e il seno per quel valore.
Pertanto, se si guarda la linea di pi/3 nel primo quadrante, il coseno di cos(pi/3), è uguale a 1/2
Quando guardi la linea pi/6 nel primo quadrante, cos(pi/6) è uguale a sqrt3/2
Quindi la moltiplicazione di cos(pi/3)*cos(pi/6) sta semplicemente moltiplicando semplici frazioni.
1/2*sqrt3/2=sqrt3/4

