di

Qual è la componente Z del momento angolare orbitale? Come possiamo trovare il componente Z? Qual è la sua importanza? A cosa assomiglia?

Sembra che ti stia riferendo a #m_l#, che è il valore osservato che corrisponde a #z#-componente del momento angolare orbitale totale #L_z#.

In pratica, per la chimica generale, puoi semplicemente usare il valore di #l# come la gamma di #m_l#ed esprimere #m_l# come:

#bb(m_l = {-l,-l+1, . . . , 0, . . . , l - 1, l})#

Ad esempio, se #l = 2# (come per a #d# orbitale), quindi:

#m_l = {-2,-1,0,+1,+2}#

Ciò significa cinque #d# esistono orbitali per un dato numero quantico principale #n#:

http://2012books.lardbucket.org/

RAPPORTO CON IL COMPONENTE Z DEL MOMENTO ANGOLARE TOTALE ORBITALE

Ricordiamo che l'equazione di Schrodinger è tipicamente scritta come #hatHpsi = Epsi# (dove #E# è l'energia, #hatH# è l'operatore hamiltoniano e #psi# è la funzione d'onda).

Bene, si scopre che #psi#, la Funzione d'onda descrivendo lo stato di un sistema meccanico quantistico, può essere separato in a radiale e del angolare componente, #R_(nl)(r)# e #Y_(l)^(m_l)(theta,phi)#:

#psi_(nlm_l)(r,theta,phi) = R_(nl)(r)Y_(l)^(m_l)(theta,phi)#

where #n#, #l# e #m_l# sono il principale, il momento angolare e il magnetico numeri quantici, Rispettivamente.

Tradizionalmente, #m_l# è definito come #z# componente del momento angolare #l#, ed è il eigenvalue (la quantità che ci aspettiamo di vedere ancora e ancora), in unità di #ℏ#, della funzione d'onda, #psi#.

Questo autovalore corrisponde al operatore for #L_z# e #L_z# is il #bb(z)# componente del totale momento angolare orbitale.

Quello che abbiamo appena detto può essere espresso come:

#stackrel("Operator")overbrace(hatL_z)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi)) = stackrel("Eigenvalue")overbrace(m_lℏ)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi))#

If #L_z# è ciò che intendi, quindi il significato è che lo è il fenomeno che possiamo osservare che corrisponde al numero quantico magnetico # m_l#.

PROSPETTIVA FISICA

Visivamente, in presenza di un campo magnetico nel #z# direzione, una rotazione nucleare (esibendo a momento angolare orbitale totale) si verifica lungo il #z# asse, chiamato "precessione di Larmor".

Questo è l'evento descritto da #L_z#.

Ad esempio, quando #l = 1#, come per a #p# orbitale, #m_l = {-1,0,+1}#. La "precessione di Larmor" che si presenta è simile alla seguente per a #2p_z# orbitale:

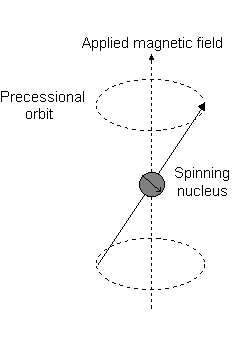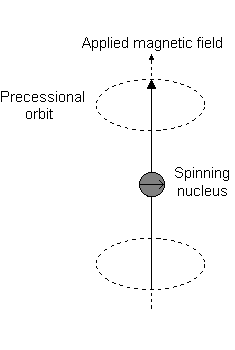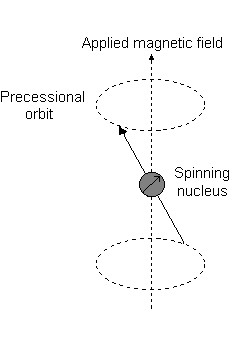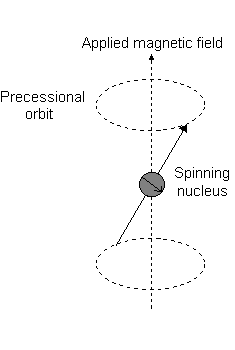
teaching.shu.ac.uk

E ciascuno #m_l# corrisponde alla distanza dal #z# asse in unità di #ℏ#:

http://hyperphysics.phy-astr.gsu.edu/

Per esempio:

  • An #m_l# of #1# corrisponde alla metà superiore del #2p_z# orbitale.
  • An #m_l# of #0# è il punto all'origine.
  • An #m_l# of #-1# corrisponde alla metà inferiore.

PROSPETTIVA DELLA CHIMICA

Da un punto di vista pratico, ciò che ci interessa davvero è come usarlo #m_l#. Ogni #m_l# corrisponde a un orbitale unico in una particolare conchiglia. Così:

  • Il numero di #m_l# valori indica il numero di orbitali in una subshell.
  • La gamma di #m_l# si basa sul prescelto #l#.

Ad esempio, da allora #l = 2# è per a #d# subshell, quindi:

#m_l = {-2,-1,0,+1,+2}#

Ciò significa cinque #d# esistono orbitali per un dato numero quantico principale #n#:

http://2012books.lardbucket.org/

Lascia un commento