Come calcoleresti la tensione superficiale di una soluzione al 2% (p / v) di un agente bagnante che ha una densità di 1.008 g / mL e che sale 6.6 cm in una provetta capillare con un raggio interno di 0.2 mm?

Un metodo per misurare la tensione superficiale di un liquido è misurare l'altezza che il liquido aumenta in un tubo capillare.

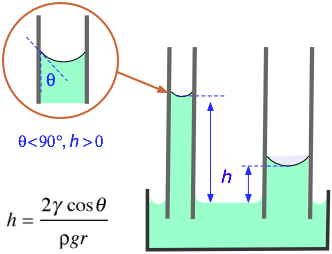
La formula è

#color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/"2cosθ" color(white)(a/a)|)))" "#

where

#γ# = la tensione superficiale
#r# = raggio del capillare
#h# = l'altezza del liquido nel capillare
#ρ# = il densità del liquido
#g# = l'accelerazione dovuta alla gravità
#θ# = angolo di contatto con la superficie

Per acqua pura e vetro pulito, l'angolo di contatto è quasi zero.

If #θ ≈ 0#, poi #cosθ ≈ 1#e l'equazione si riduce a

#color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/2 color(white)(a/a)|)))" "#

Nel tuo problema,

#r = "0.2 mm" = 2 × 10^"-4"color(white)(l) "m"#
#h = "6.6 cm" = "0.066 m"#
#ρ = "1.008 g/mL" = "1.008 kg/L" = "1008 kg·m"^"-3"#
#g = "9.81 m·s"^"-2"#

#γ = (2 × 10^"-4" color(red)(cancel(color(black)("m"))) × 0.066 color(red)(cancel(color(black)("m"))) × 1008 color(red)(cancel(color(black)("kg·m"^"-3"))) × 9.81 color(red)(cancel(color(black)("m·s"^"-2"))))/2 × ("1 J")/(1 color(red)(cancel(color(black)("kg")))·"m"^2color(red)(cancel(color(black)("s"^"-2"))))= "0.065 J·m"^"-2" = "65 mJ·m"^"-2" #

Per confronto, la tensione superficiale dell'acqua pura a 20 ° C è #"73 mJ·m"^"-2"#.