In che modo la velocità dell'onda di una stringa è uguale al calcolo della velocità usando la cinematica?
Può essere così
#v = sqrt(F_T/μ)#
#v = lamdaf" "#questa equazione è correlata all'equazione precedente
#f = 1/"time required to cover a wavelength"#
#lamda = "wavelength"#
#therefore v = 1/"time required to cover a wavelength" * "wavelength"#
#v = (cancel"(wave)" "length")/("time required to cover" cancel("a wave")"length")#
#therefore v = "length"/"time"#
La velocità dell'onda è uguale alla velocità dell'onda perché le onde stazionarie si muovono solo in una direzione.
Per capirlo dobbiamo derivare
#sqrt(F_T/u) = ω/k#
Consideriamo che una stringa con massa per unità di lunghezza è μ. È allungato da una tensione T, che è molto più grande del peso della corda e la sua posizione di equilibrio è lungo l'asse x. Questo diagramma mostra una breve sezione della corda, allungata nella direzione x, e le forze che agiscono su di essa. La nostra analisi si applica solo a piccole deformazioni, per le quali la corda è un mezzo lineare e trascuriamo la forza gravitazionale sulla corda (che in ogni caso è costante).
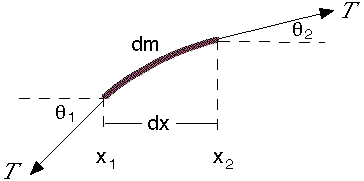
Una conseguenza di questa limitazione alle piccole deformazioni è che l'angolo θ tra la stringa e la direzione x è molto più piccolo di 1, quindi #sin θ ≅ θ and cos θ ≅ 1#. (Nel nostro diagramma, tuttavia, la deformazione è stata esagerata per chiarezza.) Ne consegue anche che la lunghezza del segmento mostrato è dx.
Appliciamo la seconda legge di Newton nella direzione verticale y:
#F_y = ma_y#
La somma delle forze nella direzione y è
#F_y = T sin θ2 − T sin θ1.#
Usando l'approssimazione dell'angolo piccolo, sin θ ≅ tan θ = ∂y / ∂x. Quindi possiamo scrivere:
#F_y = T((∂y)/(∂x))_2 - T((∂y)/(∂x))_1#
Quindi la forza totale dipende dalla differenza di pendenza tra le due estremità: se la corda fosse dritta, indipendentemente dalla sua pendenza, le due forze si sommerebbero fino a zero. Ora andiamo quantitativi. La massa per unità di lunghezza è μ, quindi la sua massa #dm = μdx#. L'accelerazione nella direzione y è il tasso di variazione della velocità y, quindi
#a_y = (∂v_y)/(∂t) = ( ∂y^2)/(∂t^2)#.
Quindi possiamo scrivere la seconda legge di Newton nella direzione y come
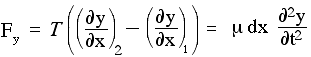
Riorganizzare questo dà
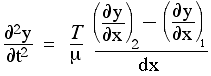
Ora stiamo usando il pedice 1 per identificare la posizione xe 2 per identificare la posizione #(x+dx)#. Quindi il numeratore nell'ultimo termine a destra è la differenza tra le (prime) derivate in questi due punti. Quando lo dividiamo per #dx#, otteniamo il tasso di variazione del primo derivato rispetto a #x#, che è, per definizione, la seconda derivata, quindi abbiamo derivato l'equazione delle onde:
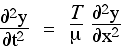
Quindi l'accelerazione (a sinistra) è proporzionale alla tensione T e inversamente proporzionale alla massa per unità di lunghezza μ. È anche proporzionale a #(∂y^2)/(∂x^2)#. Quindi una maggiore curvatura nella corda produce una maggiore accelerazione e, come abbiamo visto, una porzione dritta non è accelerata. Questa è l'equazione delle onde in una dimensione. Ora è tempo di risolverlo.
Una soluzione all'equazione delle onde
Questa è un'equazione differenziale parziale. Una delle tecniche più popolari, tuttavia, è questa: scegliere una funzione probabile, testare per vedere se è una soluzione e, se necessario, modificarla. Quindi, usiamo ciò che già sappiamo. Sappiamo che le onde sinusoidali possono propagarsi in un mezzo monodimensionale come una stringa. E sappiamo che qualsiasi funzione #f(x − vt)# è un'onda che viaggia a velocità v. Nel primo capitolo sulle onde che viaggiano, abbiamo visto che una versione elegante dell'espressione generale per un'onda sinusoidale che viaggia nella direzione x positiva è# y = A sin (kx − ωt + φ)#. Una scelta adeguata dell'asse xo ci consente di impostare φ su zero, quindi diamo un'occhiata all'equazione
#"y" = "A sin"(kx - ωt)#
per vedere se e quando questa è una soluzione per l'onda
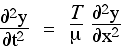
Nel prendere la derivata parziale rispetto a t, manteniamo costante x e viceversa. Quindi, ricordando che la derivata di seno è cos e che la derivata di cos è meno seno, possiamo scrivere le prime due derivate parziali rispetto a t e x in questo modo:
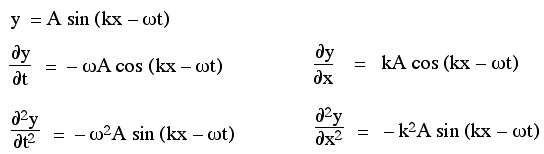
Velocità dell'onda in una corda allungata
Quindi abbiamo visto che i secondi derivati parziali hanno la forma corretta, il che significa che siamo sulla strada giusta. Tuttavia, per essere una soluzione a
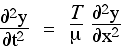
i derivati parziali

#ω/k = sqrt(F_T/μ)#
Per capire da dove viene questa equazione, considera un'onda sinusoidale di base,# A cos (kx−ωt)#. Dopo il tempo t, la sorgente ha prodotto oscillazioni ωt / 2π = ft#(omega = 2pif)#. Dopo lo stesso tempo, il fronte d'onda iniziale si è propagato dalla sorgente attraverso lo spazio alla distanza x per adattarsi allo stesso numero di oscillazioni, kx = ωt.
Quindi la velocità di propagazione v è #v = x/t= ω/k#. L'onda si propaga più velocemente quando le oscillazioni di frequenza più elevata sono distribuite meno densamente nello spazio. [2] formalmente, #Φ = kx−ωt# è la fase. Da #ω = (−dΦ)/(dt)# e #k = (+dΦ)/(dx)#, la velocità dell'onda è #v = (dx)/(dt) = ω/k#
E come
#k = 2pie" "e = 1/lamda#
Dove e è la frequenza spaziale
#k = (2pi)/lamda#
Quindi
#w/(2pi)/lamda = f/lamda#

